テスト番号VS13中間点に荷重がかかるピン留めされた梁に対する最大変位と応力を求めます。
定義
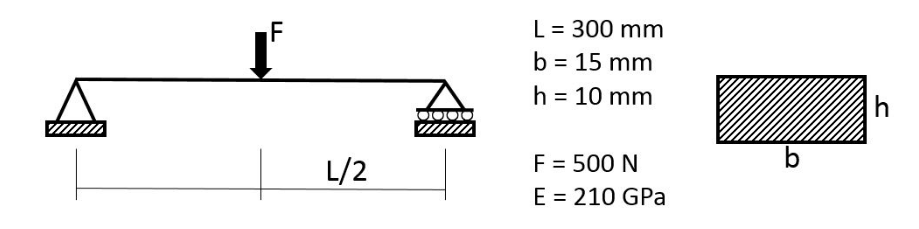
図 1.
単位はSIです。
結果
最大変位に対する基準解は以下のように与えられます:
(1)
ここで、
-
最大変位に対する基準解は以下のように与えられます:
(2)
ここで、
-
以下の表は、変位と応力の結果をまとめたものです。
| |
基準 |
SimSolid |
%差異 |
| 最大変位 [mm] |
1.0714E+00 |
1.0764E+00 |
0.46% |
| 最大応力 [MPa] |
1.5000E+02 |
1.5011E+02 |
0.07% |

